How Algorithms ACTUALLY work on the Rubik’s Cube
公式是如何在魔術方塊的解法中運作的?
文章內容來源皆來自以下影片:
J-Perm – How Algorithms ACTUALLY Work on the Rubik’s Cube
我認為這部影片充份解釋了對於魔術方塊公式的運作原理跟迷思
希望能夠讓未曾接觸過魔術方塊的大眾朋友對於公式有更深一層的認識
關於公式
On the Rubik’s Cube an algorithm
is any sequence of turns used to achieve a goal.
This could be something as simple as
flipping a piece during the cross
or making the cross on the top face,
or do something as advanced
as solving the entire last layer at once.
Algorithms are written like this where each letter
tells you which face to turn clockwise
or counter-clockwise if there’s a prime on it
or turn it twice if there’s a two.
In the CFOP speedsolving method
the last two steps are entirely solved using algorithms.
在魔術方塊領域中,
「公式」可以是任何一段用於達成目標的轉動順序
它可以像是單純把十字的某個邊塊方向翻動
或是把十字的所有邊塊放到頂面這麼簡單
或是更進階一點一口氣把整個最後一層給解完這麼複雜
「公式」會用特定的英文代號告訴你
什麼時候該把哪些面轉順時針,什麼時候該把哪些面轉逆時針
又或是什麼時候該把哪些面轉 180 度…等等
在最普及的速解法:CFOP 解法當中
最後兩個步驟 – OLL & PLL 就是完全用公式來解開的
為什麼要用公式這個稱呼?
Now quick side note :
The word “Algorithm” outside of cubing
is more supposed to mean steps
that may change depending on the situation,
so not exactly a set sequence of steps.
And a more appropriate word would be
something like “sequence” , but in cubing
we like to use big words to impress people
because for some reason
solving a cube is not impressive enough.
先讓大家有個認知:「公式」這個名詞
如果不用在魔術方塊的領域中解釋
則會有「根據情況而改變的步驟」之意義
所以並不全然是固定的轉動順序
更適合的用詞應該是「序列」
但是在魔術方塊領域中
我們喜歡用更吸引人注意的用詞來對圈外人推廣
因為某種程度上來說,會解一顆魔術方塊
其實不太能吸引到什麼注意…
不一定所有情況都需要套公式
The earlier stage of solving the cube
is more intuitive and that means
you can figured it out as you’re solving.
For example to solve the first two layers
I need the red and blue pieces in here
which they are currently over here
I can put them together with three moves
and then I can move it to the front
and put it in here with three moves.
在解開魔術方塊的前幾個步驟
其實是比較能夠直覺完成的
代表著你可以自行推導目前的狀況該怎麼處理
舉個例子,以 F2L 來說我可以用簡單幾個動作
讓某個角塊從原處移動到我想要它移動過去的地方
並且跟相同顏色的邊塊組合在一起
最後再用另外幾個簡單動作
把這兩顆零件同時放入它們應該放入的位置
除了記憶公式,真的能夠理解嗎?
Now these are all thing I can figure out on the spot
because they are very short
and don’t really count as algorithms,
but then on the last layer
I just see this pattern and I know what to do,
and then I see this pattern and I do this.
Those are just pre-memorized sequences of moves
or algorithms that I’ve just done.
But I’ve just memorized these,
do I even understand these algorithms?
Uh…yes, sometimes.
上面講到的步驟都是我能夠推導理解的
因為它們所需要的動作非常少,甚至稱不上是「公式」
但是當我解到了最後一層的時候,
我只要看到頂面的顏色排列就能用公式一口氣完成,
頂層的復原也是看一眼就能用公式解決掉
能夠完成這些動作都是因為
事先記憶在我腦袋裡的轉動序列 – 「公式」
不過如果我只是把這些公式記住
我真的能夠搞懂這些公式在做什麼事嗎?
呃…是的,在某些時候是這樣沒錯。
第一種型態:Commutator 交換子
Okay, how do algorithms actually work,
that’s what I’m here to talk about.
There are many types of algorithms
but we’re gonna start with one
and that’s called the “Commutator”.
The basic idea of a commutator
is there are three pieces you have to
solve that in a cycle and you can
solve these all with an algorithm
that is actually quite intuitive.
You find one move that can solve
one of the pieces into the right spot,
then you put another piece into here
also in a way so that it looks
solved compared to its surroundings.
So this is the first move (D),
then this one goes here (R U’ R’) like this,
and there it is. Then you undo the first move (D’)
and undo that second sequence (R U R’).
That actually solves it and
what the commutator means is that
you are doing one thing (A) another thing (B)
and then the reverse of each of those (A’ B’).
The commutator idea is used in plenty of algorithms
you may not have realized that this one is
simply a three-corner swap because
you’re usually thinking about making yellow on top.
But it is a commutator is just done
like this (r U R’ U’ r’ F R F’)
so that the finger tricks are better.
到底公式是怎麼樣運作的呢?
那就是我們這次要討論的議題了
魔術方塊公式的運作原理有分為很多種
我們先從最基本的 「Commutator 交換子」概念開始講起
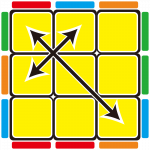
 <— 三顆角塊需要交換
<— 三顆角塊需要交換
Commutator 最基本的觀念是當你有三顆零件需要復原
而你可以用很直覺的方式解開這個情況
你找到一個轉動動作可以讓
其中一塊 A 零件移動到正確的位置,
然後你再把另一顆 B 零件以另外一種方式放到屬於它的位置
藉由跟周圍零件的顏色連接在一起
你能夠判斷上述這兩顆零件是被復原的
所以第一個動作是 D,將 A 零件放入
再來第二個動作是利用 R U’ R’ 把 B 零件放入
接下來你只需要把第一個動作倒轉 D’
再把第二個動作倒轉 R’ U R
就能夠完成三顆零件的交換了
簡單地描述 Commutator 的概念
就是 [ A B A’ B’ ]而已 (A’ 為 A 的倒轉動作,B’ 同理)
你可能沒有發現其實 Commutator 的原理
應用在相當多的公式中,而這裡提到的
只是其中一個最簡單的三角交換情況
因為在這時你會去注意到的東西
應該只有讓頂面的顏色全部回到上面復原
 <— 換方向操作就會改變轉法
<— 換方向操作就會改變轉法
原本的公式 D – R U’ R’ – D’ – R’ U R
也有可能被改寫為 r – U R’ U’ – r’ – F R F’
這只是為了因應能夠更順暢地操作指法而做的更動
第二種型態:Conjugate 共軛
Another type of algorithm is a conjugate,
this algorithm (R U R’ F’ R U R’ U’ R’ F R2 U’ R’ U’)
solves the J-permutation which means
these and these two have to swap with each other,
so when you do it, they end up in each other’s spots.
So in this case (Na-perm) we need to
swap these two and these two,
so all we have to do to swap these
is put them in the same spot as where
we solved a J-perm so we can just
move these like this (R U R’ U), now they are here.
Now if you do a J-perm (R U R’ F’ R U R’ U’ R’ F R2 U’ R’ U’)
to solve these then undo those four moves (U’ R U’ R’),
then you will solve that case.
That is a conjugate because we’re doing
a setup move (A) into an algorithm (B)
and then undoing the setup move (A’),
that allows us to solve a variety of
cases using the same base algorithm.
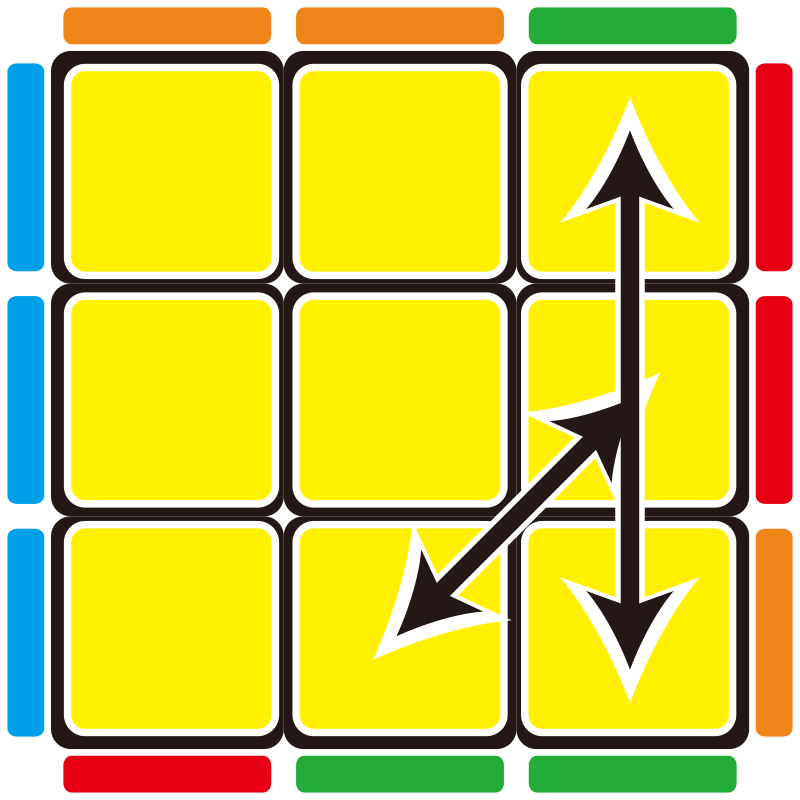
另一種公式運作方法是 「Conjugate 共軛」,
舉Jb-perm作為例子 – 可以先將解好的方塊
操作 R U R’ F’ R U R’ U’ R’ F R2 U’ R’ U’ 來做出這個排列狀況
可以看到J-perm的狀況是右側兩顆角塊,
以及右 & 前方的邊塊需要交換
所以當你操作 R U R’ F’ R U R’ U’ R’ F R2 U’ R’ U’ 這串公式時
所有的零件都會回到各自的位置上
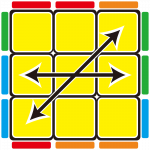 —>
—> 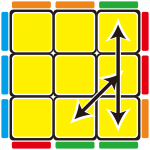
當你遇到Na-Perm的交換情況
會是左前方 & 右後方的角塊,
以及左右兩側的邊塊需要交換
所以我們可以利用幾個簡單的動作 R U R’ U
將這些需要交換的邊角們
都移動到 Jb-perm 的排列位置,這裡稱之為 Setup
然後再操作 Jb-perm 的公式 R U R’ F’ R U R’ U’ R’ F R2 U’ R’ U’
等交換完所有的邊角之後
再把一開始 Setup 的動作倒轉回來 U’ R U’ R’
就能夠解決這個狀況
這種做法就稱為 Conjugate 共軛
因為我們是先將遇到的情況做一個 Setup 動作 A,
使其變成 B 的狀況,等到用 B 的原有公式解決之後
再以倒轉的 Setup 動作 A’ 來復原
簡寫為 [ A B A’ ],這樣的運作方法
得以讓我們用相同的基底公式來解決多種情況
第三種型態:破壞與重組
Another type of algorithm is Destroy & Repair.
You may seen this algorithm before (R U R’ U R U2 R’)
and how it works is like this,
the first three moves (R U R’) take out this F2L pair,
so what we’ve done is we’ve destroyed F2L
but we’re going to repair it just obviously not the same way
because that would do nothing
but we’re going to repair it a different way (U R U2 R’),
and how that’s done by moving the pair further away (U)
and moving it all back in (R U2 R’) like this.
And that actually changes what the top looks like in this case it solved it.
And here you can solve this OLL (R U R’ U’ R’ F R F’)
to make it all yellow on top by taking out this pair (R U R’ U’)
then putting it in a different way, in this case this way (R’ F R F’).
You can get pretty crazy with the idea
of destroy and repair and it
doesn’t just apply to the F2L slot,
sometimes you can mess up
multiple F2L slots (R U R’ U R’ U’ R)
and then try to put them back together (R U’ R’ U R’ U R),
and sometimes what you’re destroying
is OLL (F R U’ R’ U’ R U R’ F’) and then
you’re solving it with a different OLL case(R U R’ U’ R’ F R F’).

還有一種公式運作方法是
「Destroy & Repair 破壞與重組」
你可能曾經看過這條公式:
R U R’ U R U2 R’ (俗稱小魚公式)
而這條公式就是以這種破壞重組的概念推導的
前三個動作 R U R’ 是將右前方的
F2L Pair 取出,也就是「破壞」
而我們不可能單純把這三個動作倒轉回去
那樣就什麼事也不會發生了
反之我們會用其他的方式
將這組 F2L Pair 重新放回去
所以第四個動作我們先將
這組 F2L Pair 轉個 U 推得更遠一點
再轉動 R U2 R’ 這三個動作
把它放回去,也就是「重組」
而這樣的破壞重組 F2L Pair 的過程
我們可以看到頂層的顏色被復原了
如此一來得到證明
之後遇到這種情況時
可以用 R U R’ U R U2 R’ 來解決

另外在遇到OLL 33這種情況時
若想要一口氣完成整個頂面的黃色
你可以操作 R U R’ U’ R’ F R F’ 來完成
而操作的過程是先以 R U R’ U’ 把右前方的 F2L Pair 取出
並且用別種方法放回原位
在這裡的情況是使用 R’ F R F’ 來復原
更進一步的推理
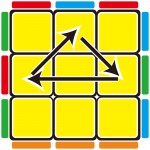
如果你有勇氣願意嘗試更瘋狂的點子
例如Ua Perm的這個方向的做法
有別於只是把單一個 F2L Pair 取出
你可以同時破壞多個 F2L Pair (R U R’ U R’ U’ R)
再嘗試把這些移出的 F2L Pair 重新放回去 (R U’ R’ U R’ U R)
 +
+  =
= 
或者是當遇到 Y-Perm 時
你可以用 OLL 37 的公式 F R U’ R’ U’ R U R’ F’來破壞
會發現方塊變成 OLL 33 的情況
只需要再以 OLL 33 專用的公式 R U R’ U’ R’ F R F’ 復原
就能夠解決 Y-perm 了
理解過程還不算 100 % 搞懂?
Okay, so you can see why break and repair
it dosen’t destroy the previous step
because you then go and repair it,
but why does doing this sequence
of two OLLs (F R U’ R’ U’ R U R’ F’) + (R U R’ U’ R’ F R F’)
lead to solving this PLL case specifically?
How does it all work?
Well, here’s the thing…I don’t know.
I mean I can do the algorithm really slowly
and trace over all the pieces for you
and show you where they all ended up,
but that’s not really an explanation is it?
It’s a proof that the algorithm works
but it doesn’t give you like
a satisfying reason why it works.
經過上面的說明,你可以明白
為什麼用 Destroy & Repair 這種公式運作原理
並不會把更前面做好的步驟給弄亂
因為你在破壞的動作結束之後馬上就進行重組了
 +
+  =
= 
但問題在於,為什麼 OLL 37 + OLL 33 這兩個公式的組合
可以專門拿來處理 Y-Perm 的狀況呢?這到底是如何辦到的?
坦白說,我也不知道。
換句話說,我能夠將公式轉動執行得非常緩慢
慢到能夠讓我的眼睛追蹤到每一塊關鍵零件的移動
而且能夠跟你說明最後那些零件會回到哪去
但我想這並不是一個完整的解釋
將公式操作完畢之後能夠解決狀況
只是證明了這樣的轉法行得通
卻沒有辦法給你任何滿意的理由說明它是如何做到的。
人腦 vs 電腦
My brain is a human brain and so is yours,
and we can’t comprehend what is
actually happening after this many moves.
A lot of our algorithms are found
through just trying stuff on the cube
(R U R’ + U R U’ R’ U + R U2 R’)
and seeing what works
but a lot of them are also found
through the help of computers,
and actually computers don’t even
really understand what’s going on.
A lot of the time it’s just trial and error,
so if a computer is just doing trial and error
and then that’s how they discover these,
then how are we ever supposed to
understand what’s going on?
我的腦袋是人類的腦袋,你的也是,
而我們身為人類,並沒有辦法去理解
在轉了這麼多動作之後到底發生了什麼事
很多公式被發現的來源是
透過不斷的在轉動過程中嘗試錯誤
並且看看哪種做法可行

例如 OLL 21 的其中一種做法
就是 R U R’ 拿出來 + U R U’ R’ U 嘗試移到別處 + R U2 R’ 放回去
但非常多的速解公式都是透過電腦運算去找出來的
事實上,電腦本身也不知道到底現在是什麼情況
很多時候只是單純的嘗試錯誤
所以連運算能力這麼強的電腦都只是在嘗試錯誤
在無數個暴力計算的結果中找到這些公式的
區區人腦如我們,怎有能力去完全弄懂來龍去脈呢?
魔術方塊的排列組合
I can understand how a few moves work,
but with each move that you add to an algorithm,
there are exponentially more possibilities
to how many cases can show up as a result.
There are 43,252,003,274,489,856,000 (43 Quintillion)
possible position on the Rubik’s Cube
and if that number is hard to visualize in terms of people,
it would be like if every person on earth had their own earth.
That’s how many positions are possible on the Rubik’s Cube,
and how many moves does it take to reach that many positions?
You only need a maximum of 20.
All that is to say the complexity of a Rubik’s Cube
as you go up in number of moves is
simply too much for a human brain to completely understand.
我的腦袋能夠理解短短幾步動作是如何進行的
但是每當這串動作被多加上一個、兩個….數個動作的同時
狀況的複雜度也會呈現指數性的爆增
一顆 3×3 魔術方塊可呈現的排列組合
總共有 43,252,003,274,489,856,000 (43 x 10^18次方) 種
這樣的天文數字是很難以具體的描述到底多到什麼程度
真要形容的話,大概就是這地球上的每一個人,
手中都還握有一個地球的總人數吧
這就是魔術方塊全部的排列組合數量
而要轉幾個動作才能達到這樣的排列組合數字呢?
你只需要最多 20 步就能夠達成。
說了這麼多都是要告訴大家,
當你轉動魔術方塊越多下的同時,
排列組合的複雜度隨時都有可能
爆增到人腦無法完全理解的程度。
「Commutator 轉換子」
I fully understand commutator
but it took me a while to grasp it,
and even when I move up to challenges
where I solve bigger cubes in weird ways,
I still use commutator because I can
rely on them as I completely understand how they work.
But when it comes to something like break and repair,
I understand the concept of why this produces useful algorithms,
but I don’t understand any of what happens in that algorithm.
So sometimes you’ll still see me use this
technique such as on Square-1 or Skewb,
but that’s only because I had no clue what was going on.
I just tried breaking and repair
and I tried it enough times that it
created a useful algorithm.
But I don’t actually understand
what I’m doing when I do use it.
Basically you will never fully understand
all of the algorithms that you’re using.
The way that they work is simply too
complex for the human brain to grasp.
我完全理解 Commutator 交換子的概念
但也花上了我不少時間去掌握
而當我在挑戰用奇怪方法解超高階魔術方塊時
我也一樣使用 Commutator 去完成
因為我完全能夠知道它是怎麼運作的
但是當面對破壞重組的運作原理時
我能夠明白為什麼這種原理可以推導出有用的公式
卻無法對於中間發生了什麼事透徹理解
所以有時候你會看到我利用這種
破壞重組的概念在解 Square-1 或是 Skewb
但說真的在嘗試的過程中我不知道我在幹嘛
基本上你不可能 100% 理解你目前所使用的全部公式
有些公式的來龍去脈對於正常人腦來說已經太過難以掌握了
轉得快就只是背公式嗎?
So then why??
Why do cubers learn these algorithms
and then try and impress other people
by their solving? Isn’t that a bit fake?
We don’t really know what’s going on,
we’re just memorizing it.
Speed Cubing is less about the CUBE
and more about the SPEED,
and if all you think that means
is move your fingers really really fast,
that doesn’t matter if you’re
doing way too many moves for something
that can be solved in fewer moves,
or if you do a cube rotation
to force easier finger tricks rather than just using more
creative finger tricks that allow you to solve the case faster.
You also want to avoid something
as simple as changing your grip
on the cube as that is time spent not turning.
Make sure that while you’re doing one algorithm
you can watch the fast moving pieces
on another part of the cube,
so you can begin the next algorithm
without having to pause.
Oh, when you trying to figure out
where each piece goes to know what algorithm to do.
Well, just look at the colors on the front
and that should be enough to tell you what to do.
所以…為什麼速解玩家要花這麼多時間記憶這些公式
就為了在其他人面前轉得更快一點吸引大家的注意呢?
這是不是有一點虛偽了呢?
我們其實根本不知道究竟發生什麼事
我們只是把公式記起來而已
「速解」一詞的重點比較不在於「解」這個字,
更多比重是在於「速」的,
你可能認為這只需要讓手指頭動得更快一點就好
但事實上就算手速再快,
若你的解法是花了比最佳解多出更多步數的做法,
那單純高手速就沒有什麼幫助
你可能還需要去研究同一種情況
究竟是要翻動方塊以操作更簡單快速的指法
還是要使用更花俏更高效率的指法
來讓你復原的速度更快一點
另外你應該也需要去嘗試避免過多的重新抓握方塊
因為在手離開方塊的時間,方塊本身是不會轉動的
但時間依然在過,因此會影響復原的效率
想要解得更快,你還必須隨時讓眼睛能跟上
在操作公式時每個色塊的移動,
這樣才能在操作下一個公式之前
就迅速判斷出狀況,不會有停頓的現象發生
至於當你在搞清楚操作公式的過程中哪個色塊會怎麼移動
其實只要專注的看著你眼前那一面的顏色
就有足夠資訊告訴你接下來該怎麼做了
速解不僅僅是公式背得多而已
So do cubers just memorize algorithms
without even understanding what they do?
YES, for part of the solve,
and memorization is only one of many aspects.
Just memorizing the algorithm is not what’s going to make you fast,
you do have to memorize some stuff and
it maybe a little painful but that’s how you gain
access to an entire new world of possibilities.
所以,速解玩家們真的只是把公式記起來
卻沒有去完全理解他們在做什麼嗎?
是的,在整段復原過程的某部份是這樣子的
然而「記憶」只是在提升速解效率的多項因素中的其中一環
光是把公式記起來並不會讓你變得更快
還有更多更重要的關鍵是你必須學習的
記憶公式固然是需要花費時間,而且令人煩躁苦悶的
但是這也是讓你在速解領域踏入全新境界的必經之路。